miércoles, 18 de junio de 2014

En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y(llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).
En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”.
Las funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso.
A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?:
                          1 -------->   1
                          2 -------->   4
                          3 -------->   9
                          4 --------> 16
Los números de la derecha son los cuadrados de los de la izquierda.
La regla es entonces "elevar al cuadrado":
                           1 -------->   1
                          2 -------->   4
                          3 -------->   9
                          4 --------> 16
                           x -------->   x2.

Pendiente de una recta

Pendiente: m=\frac{\Delta y}{\Delta x}=\tan( \theta )
La pendiente de una recta en un sistema de representación rectangular (de un plano cartesiano), suele estar representada por la letra m, y está definida como la diferencia en el eje Y dividido por la diferencia en el eje X para dos puntos distintos en una recta. En la siguiente ecuación se describe:
m = \frac{\Delta y}{\Delta x}

Geometría

Una recta horizontal tiene pendiente igual a 0 (cero). Cuanto menor sea el valor de la pendiente, menor inclinación tendrá la recta; por ejemplo, una recta que se eleve un ángulo de 45° con respecto al eje X tiene una pendiente m = +1, y una recta que caiga 30° tiene pendiente m = -0,5. La pendiente de una recta vertical no está definida, o se dice que es infinita.
El ángulo θ que una recta forma con el eje horizontal está relacionado con la pendiente m por medio de la siguiente relación trigonométrica:
m = \tan\,\theta
o equivalentemente:
\theta = \arctan\,m
Dos o más rectas son paralelas si ambas poseen la misma pendiente, o si ambas son verticales y por ende no tienen pendiente definida; dos o más rectas son perpendiculares (forman un ángulo recto entre ellas) si el producto de sus pendientes es igual a -1.

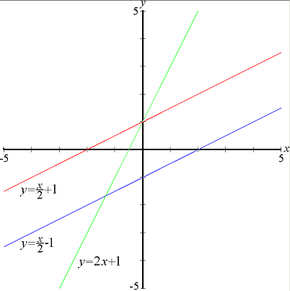
La pendiente en las ecuaciones de la recta

Tres líneas rectas — Las líneas roja y azul poseen la misma pendiente (m) que en este ejemplo es ½, mientras que las líneas roja y verde interceptan al eje y en el mismo punto, por lo que poseen idéntico valor de ordenada al origen (b) que en este ejemplo es el punto x=0, y=1.
Si y es una función lineal de x, entonces el coeficiente de x es la pendiente de la recta. Por lo tanto, si la ecuación está dada de la siguiente manera:
y = mx + b \,
entonces m es la pendiente. En esta ecuación, el valor de b puede ser interpretado como el punto donde la recta se interseca con el eje Y, es decir, el valor de y cuando x=0. Este valor también es llamado ordenada en el origen.
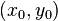Si la pendiente m de una recta y el punto (x_0,y_0) de la recta son conocidos, entonces la ecuación de la recta puede ser encontrada usando:
y - y_0 = m(x - x_0) \,
La pendiente de la recta en la fórmula general:
Ax + By + C = 0 \,
está dada por:
m = -\frac{A}{B}          
En general, un sistema con m ecuaciones lineales y n incógnitas puede ser escrito en forma normal como:

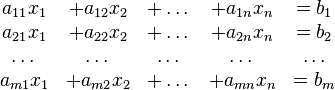\begin{matrix} a_{11}x_1 & + a_{12}x_2 & + \dots & + a_{1n}x_n & = b_1 \\ a_{21}x_1 & + a_{22}x_2 & + \dots & + a_{2n}x_n & = b_2 \\ \dots & \dots & \dots & \dots & \dots \\ a_{m1}x_1 & + a_{m2}x_2 & + \dots & + a_{mn}x_n & = b_m \end{matrix}
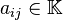Donde x_1,\dots,x_n\, son las incógnitas y los números a_{ij}\in\mathbb{K} son los coeficientes del sistema sobre el cuerpo \mathbb{K}\ [= \R, \mathbb{C}, \dots]. Es posible reescribir el sistema separando con coeficientes con notación matricial:
(1)
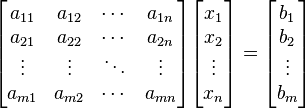 \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix}
Si representamos cada matriz con una única letra obtenemos:

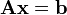\mathbf{Ax} = \mathbf{b}
Donde A es una matriz m por n, x es un vector columna de longitud n y b es otro vector columna de longitud m. El sistema de eliminación de Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el cuerpo del que provengan los coeficientes. La matriz A se llama matriz de coeficientes de este sistema lineal. A b se le llama vector de términos independientes del sistema y a x se le llama vector de incógnitas.

Los sistemas de ecuaciones lineales fueron ya resueltos por los babilonios, los cuales llamaban a las incógnitas con palabras tales como longitud, anchura, área, o volumen, sin que tuvieran relación con problemas de medida.
Un ejemplo tomado de una tablilla babilónica plantea la resolución de un sistema de ecuaciones en los siguientes términos:
1/4 anchura + longitud = 7 manos
longitud + anchura = 10 manos
Para resolverlo comienzan asignando el valor 5 a una mano y observaban que la solución podía ser: anchura = 20, longitud = 30. Para comprobarlo utilizaban un método parecido al de eliminación. En notación, sería:
y + 4x = 28
y + x = 10
Restando la segunda de la primera, se obtiene 3x = 18 , es decir: x = 6 e y = 4 .
También resolvían sistemas de ecuaciones, donde alguna de ellas era cuadrática. Los griegos también resolvían algunos sistemas de ecuaciones, pero uti1izando métodos geométricos. Thymaridas (400 a. de C.) había encontrado una fórmula para resolver un determinado sistema de n ecuaciones con n incógnitas.
Diophante resuelve también problemas en los que aparecían sistemas de ecuaciones, pero transformándolos en una ecuación lineal. Diophante sólo aceptaba las soluciones positivas, pues lo que buscaba era resolver problemas y no ecuaciones. Utilizó ya un álgebra sincopada como hemos señalado anteriormente. Sin embargo, unas de las dificultades que encontramos en la resolución de ecuaciones por Diophante es que carece de un método general y utiliza en cada problema métodos a veces excesivamente ingeniosos. Los sistemas de ecuaciones aparecen también en los documentos indios. No obstante, no llegan a obtener métodos generales de resolución, sino que resuelven tipos especiales de ecuaciones.
El libro "El arte matemático" , de autor chino desconocido (siglo III a. de C.), contiene algunos problemas donde se resuelven ecuaciones. En ellos encontramos un esbozo del método de las matrices para resolver sistemas de ecuaciones lineales. Uno de dichos problemas equivale a resolver un sistema de tres ecuaciones lineales por dicho método matricial.


Vectores en R2.
Adición de vectores.
Adición y sustracción de vectores.
Método del paralelogramo.
Producto escalar o producto punto de dos vectores.
Vectores y geometría.
Aplican de vectores a velocidades y fuerza.
Resolución de problemas.
Ciencia, Tecnología y sociedad.
Tecnología de información y la comunicación: Adición de vectores con geografía, método del poligono y del paralelogramo.
Evaluación.
Se deben utilizar las funciones del algebra de valdor y el algebra de mancil., se utilizan basicamente las funciones indicadas en las sigueientes proporciones el cual son muy faciles o complicadas cada quien tiene las funciones y relacione trigonometricas..
Publicadas por a la/s No hay comentarios.:
Suscribirse a: Entradas (Atom)